[Python Data Analysis]주성분 분석(Principal Component Analysis), 요인 분석(Factor Analysis)_PCA 코딩

*주성분 분석(Principal Component Analysis)

- 아래에서부터 위로의 분석; ‘데이터’에서 시작

- 변수의 수를 줄이는 차원 축소 기법 중 하나

- 다수의 변수를 어떻게 모아서 y에게 주는 영향을 더 잘 추정할 수 있을까? 에 대한 고민

- 고차원 데이터를 압축

  : 변수 서로서로의 상관성이 큼 -> 묶을 수 있는 변수들을 찾아서 뭉터기로 반영(x1,x2,x3 => I1하나의 뭉터기) 

- 데이터로부터 x들을 뽑아서 I들로 묶은 뭉터기로 종속변수 추정

- Eigen value, Factor Loading

-목적: 회귀분석시 독립변수 간에 (상관성이 높기 때문에) 다중공산성이 존재하는 문제 해결

- 주성분 분석 전 표준화

  : 데이터 스케일링을 하지 않으면 스케일에 따라 주성분의 설명 가능한 분산량이 달라지기 때문

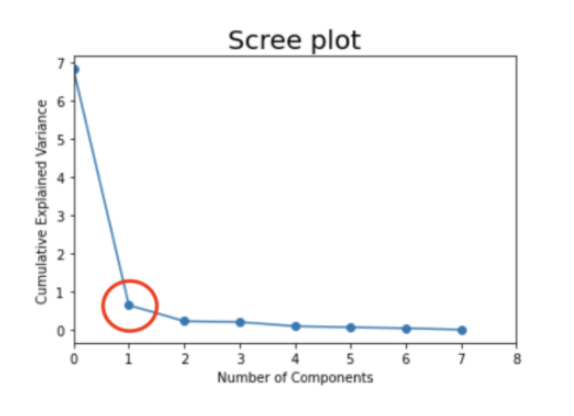
- 주성분 갯수 선택

  : Scree plot을 통해 기여율을 시각화. 급격하게 꺾이는 지점에서 주성분 개수 선택

scree plot을 통해 주성분 갯수 선택

 

 

*요인 분석(Factor Analysis)

- 위에서부터 아래로의 분석; ‘이론’에서 시작

- 수많은 변수 중에서 잠재된 몇개의 요인을 찾아내는 것

- 관측된 변수는 요인과 오류 항의 선형 조합으로 모델링됨

 

- ex) 브랜드가치 -> I1 = 신뢰감 / I2 = 만족감 / I3 = 편리함 (이론으로 부터 I를 찾음) -> I에서 x들 파생

- 정말 x들을 통해 I를 설명할 수 있는가?에 대한 문제

 

주성분(Principal Component), 요인(Factor)분석 비교그림

주성분(Principal Component), 요인(Factor)분석 비교 설명

 

 

*주성분 분석(PCA) 코딩

1) 필요 함수, 데이터 불러오기

PCA(Principal Component Analysis)

 

2) 결측값 확인하고 제거하기

.isnull().sum()

'상품_진열_위치', '상품_설명_표시'에서 결측값 발견

 

.dropna(axis = 0) -> '행 방향' 결측값 제거

'상품_진열_위치', '상품_설명_표시' 0으로 바뀐 것 확인

 

3) 표준화(데이터 스케일링)

StandardScaler 가져오기

모든 변수들 features에 넣기

y를 제외한 모든 변수를 x에 넣고 정규화 & 데이터프레임에 넣기

 

4) 주성분 분석 진행

- 결과값: 80% 이상이 되기 시작하는 주성분 갯수 찾기

- .cumsum(): 누적합

- pca.fit_transform(x)

- pd.Series(np.cumsum(pca.explained_variance_ratio_))

PCA()

주성분 갯수가 16개 일 때부터 80%의 설명률 가지기 시작

- 위에서 확인한 주성분 갯수(16)를 PCA(n_components= )에 삽입

- 데이터 프레임 column에 성분 16개의 열 이름 삽입('pca1' ~ 'pca16')