* 가설검정
- 가설? 내가 주장하고 싶은 바
- 귀무가설(H0): 전과 후가 똑같은 상태(=차이가 없다), Xa = Xb
통계적으로 검정하는 가설
-대립가설(H1): 차이가 있다, Xa ≠ Xb
내가 연구하고자 하는 목적
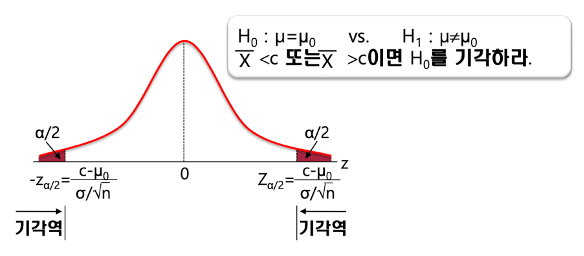
-유의확률(p-value): 어느정도를 보면 유의한가, 평균에서 완전히 벗어나 있는 끝쪽 면적
P-value가 작다(< 0.05): 대립가설 채택, 귀무가설 기각
P-value가 크다(>0.05): 귀무가설 채택, 대립가설 기각

*독립성 검정
- 데이터셋이 독립성을 따르는지 검정하는 방법
- 결과 순서대로 (검정통계량, p-value, 자유도, 기대도수)
- 귀무가설(H0): 두 변수 X와 Y는 독립적이다. (관련성이 없다)
- 대립가설(H1): 두 변수 X와 Y는 독립적이지 않다. (관련성이 있다)
- p-value < 유의수준(0.05): 대립가설 채택
*등분산성 검정
- 데이터셋의 분산이 같은지 검정하는 방법
- 귀무가설(H0): 모든 집단의 분산은 차이가 없다.
- 대립가설(H1): 적어도 하나 이상의 집단의 분산에 차이가 있다.
- p-value > 유의수준(0.05): 귀무가설 채택
1. 정규화
-이상값 처리 후 정규화 진행
-scaler: 0~1사이에 값 배정, '단위의 영향 없이' 데이터 분포(상관성)만 볼 수 있음

- preprocessing.scale()
: 자동으로 적절한 범위를 만들어서 비교가능하게 값을 할당

- MinMaxScaler()
: 0~1사이로 값을 변환해서 데이터 비교가능

- 원하는 열만 추출하여 MinMaxScaler() 적용 후 비교하기
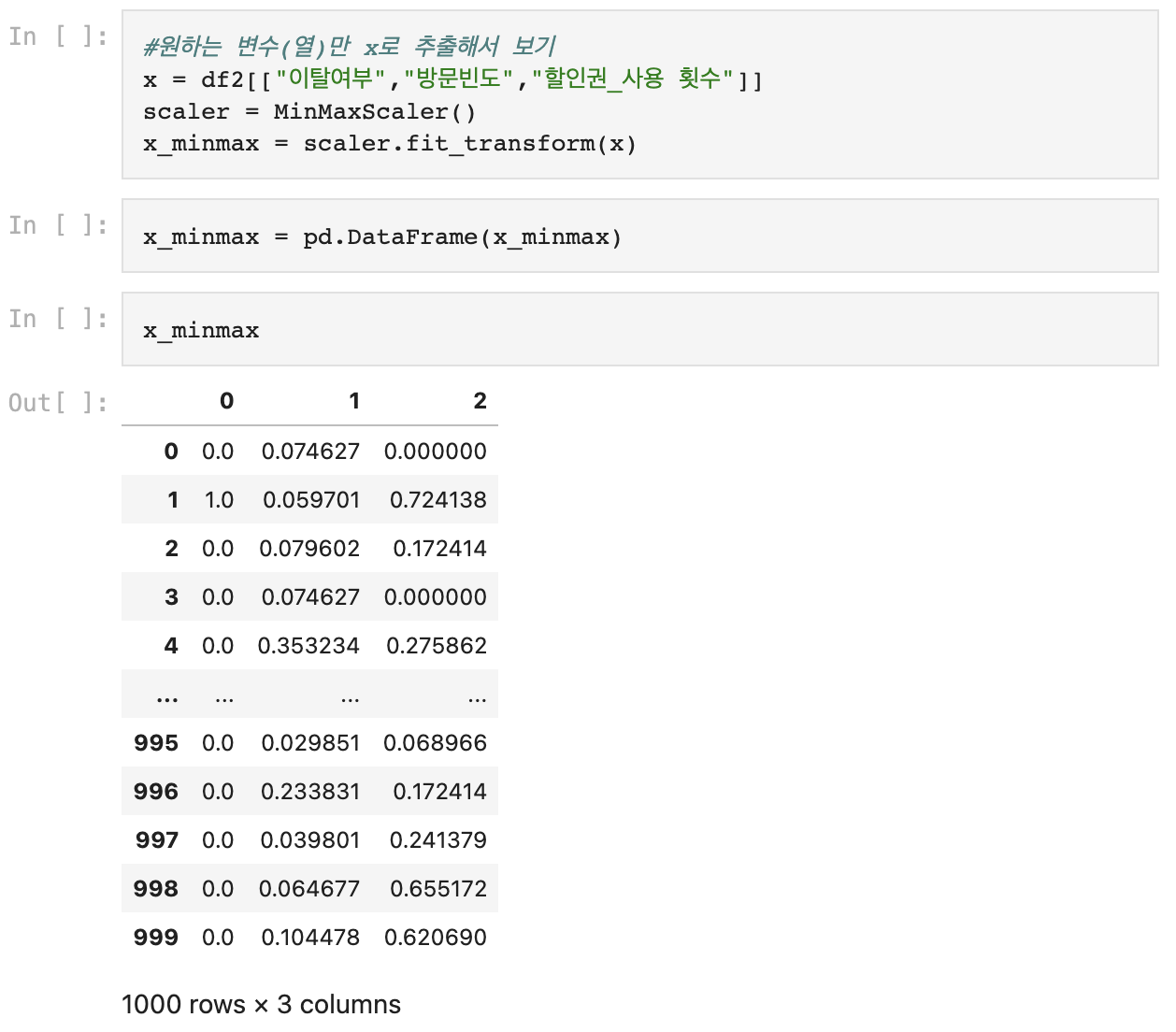
- .concat(): 데이터 합쳐서 비교해보기


2. T 검정(T-test)
- 두 집단의 ‘평균’적인 차이를 비교
- 귀무가설(H0): 두 모집단의 평균간 차이는 없다
대립가설(H1): 두 모집단 평균간 차이가 있다.
- t-value(t값): t검정에 이용되는 검정통계량

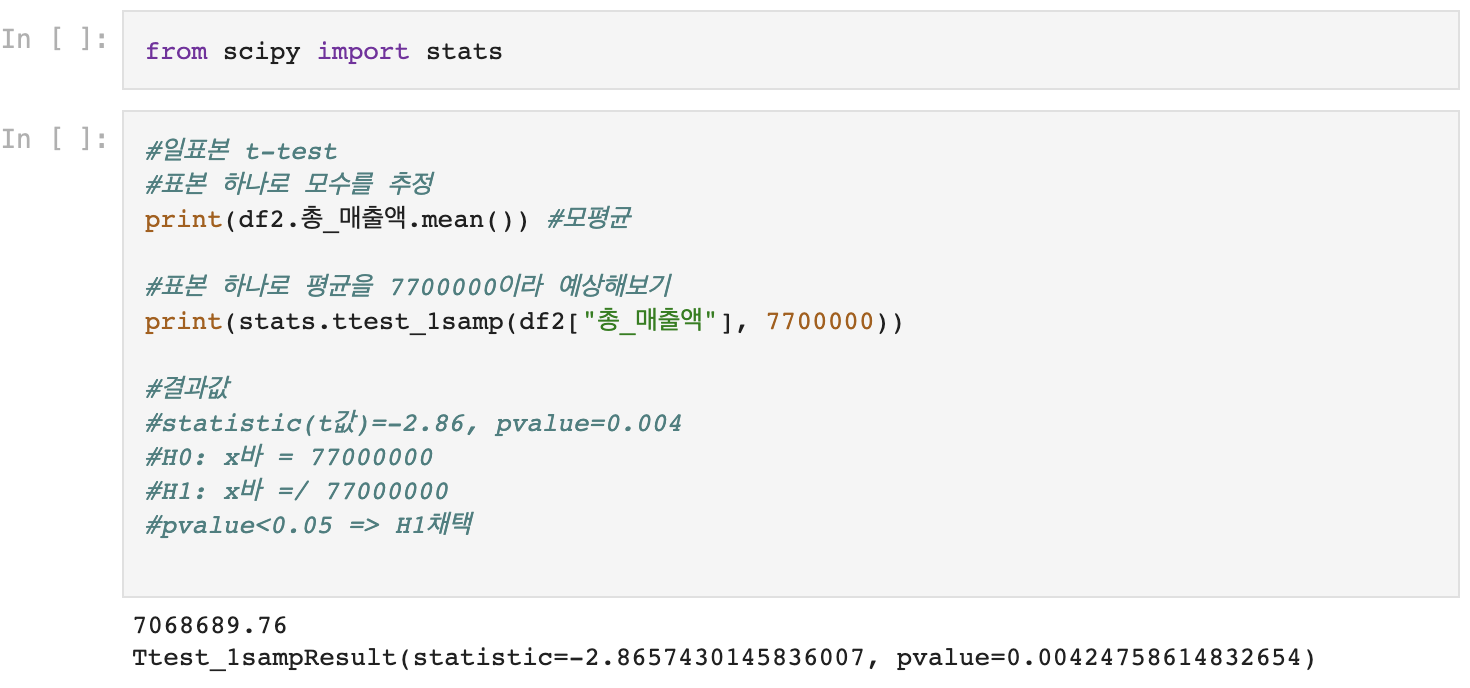
1) 일표본 t-검정
- 단일모집단에서 관심이 있는 연속형 변수의 평균값을 특정 기준값과 비교할 때 사용하는 검정방법
- 가정: 모집단의 구성요소들이 정규분포를 이룬다.
- 종속변수는 연속형
2) 독립표본 t-검정
- 두개의 독립된 모집단의 평균을 비교할 때 사용하는 검정 방법
- 가정1- 두 모집단은 정규분포를 이룬다.
- 가정2- 두 모집단은 서로 독립적, 등분산성 가정을 만족한다.
- 독립변수는 범주형, 종속변수는 연속형


3. ANOVA 분산분석
-세 집단 이상 ‘평균’비교



