* 선형 회귀 분석
- 종속변수 Y와 한 개 이상의 독립변수 X와의 선형 상관관계를 모델링하는 회귀분석기법
- 가정: 선형성, 등분산성, 독립성, 비상관성, 정상성(정규성)
- 독립변수의 갯수에 따라 1개일 경우 '단순 선형 회귀', 2개 이상일 경우 '다중 선형 회귀'로 나누어짐
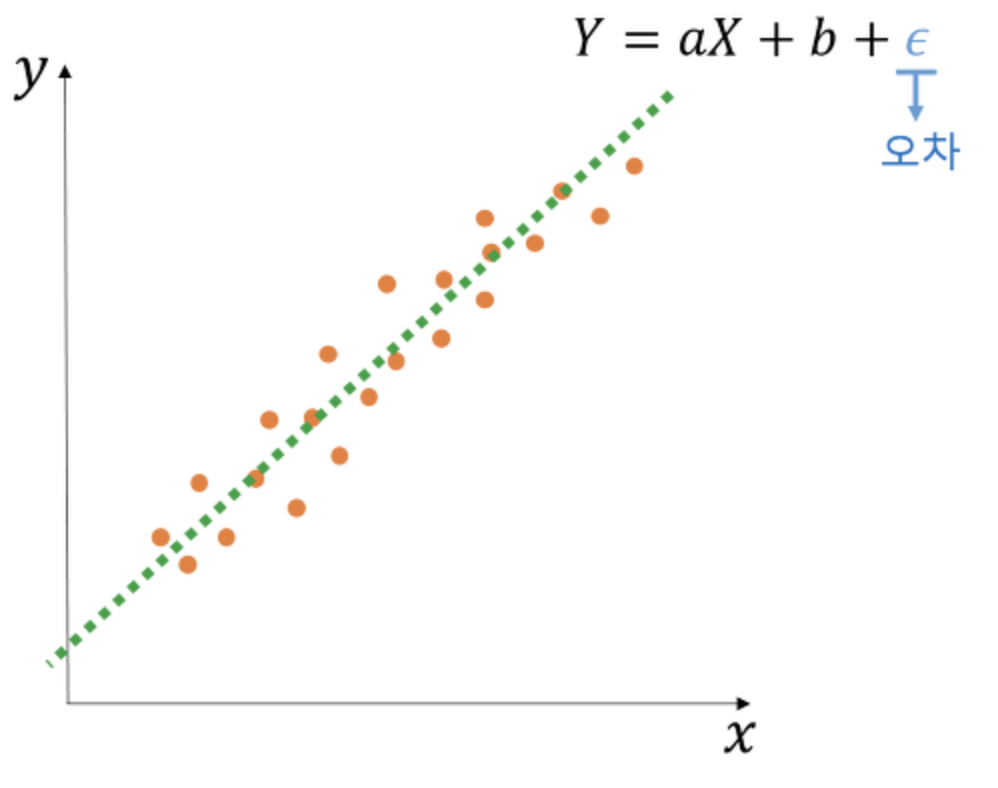

(1) 단순 선형 회귀

(2) 다중 선형 회귀

- 회귀 모델 주요 평가지표
1) MSE(평균 제곱 오차)
: 실제 값과 예측 값의 차이를 제곱해 평균한 것
: from sklearn.metrics import mean_squared_error
2) MAE(평균 절대 오차)
: 실제 값과 예측 값의 차이를 절댓값으로 변환해 평균한 것
: from sklearn.metrics import mean_absolute_error
3) R^2(결정계수)
: 분산 기반으로 예측 성능을 평가. 1에 가까울 수록 정확도가 높음
: from sklearn.metrics import r2_score
* 선형 회귀 분석 코딩
1) 필요 데이터 가져오기
- info(), describe(): 데이터의 분포, 결측치 살펴보기


2) Y에 로그 적용
- np.log1p() -> '분포를 고정'해준다.
(cf) np.log가 아닌 np.log1p를 씌우는 이유?
https://suppppppp.github.io/posts/Why-Series-MDM-1/
로그변환과 np.log()가 아닌 np.log1p()를 하는 이유
1.로그변환의 이유
suppppppp.github.io

3) 데이터 표준화 시켜주기
- 연속형 변수(num) -> StandardScaler 적용
- 범주형 변수(cg) -> OneHotEncoder 적용
: 범주형 변수들의 카테고리가 숫자로 나타나져있어서 실제로 정수를 의미하는 것이 아니지만 컴퓨터에서는 정수로 인식.
: 집단별로 쪼개서 0, 1로 인코딩 해주어 정수로 인식하지 않도록 해줌.

4) 선형 회귀 분석
- from sklearn.linear_model import LinearRegression
- 결과값 : R^2(결정계수), RMSE (평균제곱오차)-> 루트(R)를 씌운 MSE


5) 절편, 가중치 구해보기
- np.round(lr.intercept_, 3)): 절편 소숫점 3째자리까지 반올림
- np.round(lr.coef_, 3)): 가중치(beta) 소숫점 3째자리까지 반올림
